I have been away from my long time love and I want to retake my relationship with her. Yes, I am talking about you darling, so starting today I will be posting articles referencing you, my dear love: Math.
I feel in love with Math during school, however our relationship really went to the next level during my high-school senior year. I had a lot going on at the time in my life (you can read about it in my book). Up until that point I had always got Math. Almost everyone around me though, struggled with it to more or less degree, while I was cruising understanding everything and anything it threw at me.
The reason why people struggled was because they learned math by memorization, starting with the premise of multiplication tables: 2×1=2, 2×2=4, 2×3=6, and so on. Rinse and repeat for the other numbers. As Math gets harder this system falls apart because students have to memorize concepts that become unsustainable from the perspective of brute force learning through repetition.
Early on I discovered that the key to be good at Math was not to memorize; but instead, put your brain at work. By thinking and understanding how concepts worked -rather than memorizing- I was able to navigate Math’s many streams with ease. Every journey allowed me to learn from the waters, while the challenges along the way taught me how to deal with them. As you can imagine, water is dynamic and constantly changes, so I was able to learn something new with every passage. More importantly, I always employed what I had learned from my favorite movie quote of all time: “We must constantly look at things in a different way.” from Dead Poets Society.
I will never forget one of my college’s freshman year Calculus tests. It consisted of four questions: two demonstrations, one analytical exercise, and a lone harmless integral that at first glance, looked as easy as adding 2 plus 2, yet it slay wounds on the entire class… except on yours truly. Very few people were able to solve it, and the few who accomplished it were able to, not without writing several lines of trigonometric equivalencies.
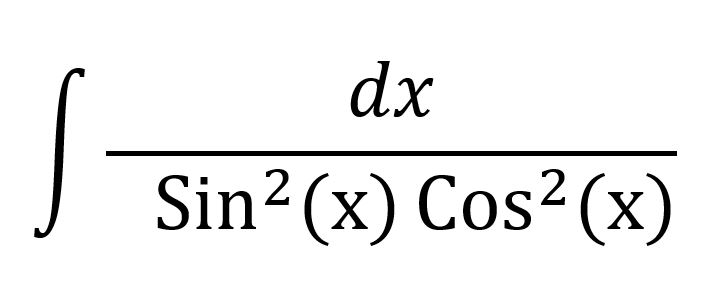
The integral was actually question #1, so it was the first thing I read on the test. As soon as I saw it, I immediately skipped to the next question, and realized the other questions required more time and effort. For a time limit of two hours in the test, I felt comfortable dedicating up to forty minutes for the other three. I knew the integral would take me less than a minute, so I figured I would solve it as soon as the professor would call “Time’s up”, during the time spent from people getting up and handing their exams. About an hour into the test I was done with questions 2, 3 and 4. It was time to get out of the classroom.
There are many lengthy ways to solve this integral. One is to use dual angle identities, such as:
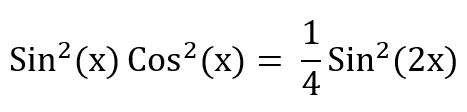
…which leads to a long series of identity equivalents to get to the solution.
You can also use:
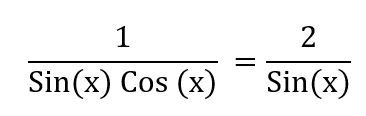
which leads to an even longer series of identity equivalencies that take you to the solution.
Or you can also apply several trigonometric properties, such as bringing…

…into the mix. All these routes would take at least fifteen minutes of vital test time, and one way or another they will get you to the solution:
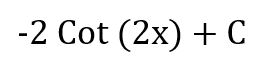
…which you can leave as is, or continue simplifying by expressing the (2x) on the numerator and denominator as function of Sin (x) and Cos (x). This is incredibly time consuming, however it was a must in our class, as professors required students to show all final solutions expressed in terms of Sin (x) and Cos (x). However, thanks to my secret weapon, I was able to get to the simplified solution on a mere two lines in less than 60 seconds (no pun intended atNicholas Cage’s film).
The key here was to rewrite the numerator… the hidden numerator… “1”:
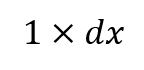
!!!!!!!!!!
The rest was to sew and sing.
Nobody, no one in the entire class solved the integral this way. To this day, I do not have a straight explanation of how I immediately determined the triviality of the integral after having visualized the solution in a matter of seconds. You have to keep in mind that circumstances are different when it comes to tests: nerves, pressure and other external factors play a crucial role that hinders your ability to think straight. Therefore I cannot speak for everyone else in my class who went through the hard way, or tried other unsuccessful methods. However, I truly believe that neither nerves, nor pressure were as key as my secret weapon of visualizing things differently.
After exiting the classroom, everyone started checking answers, and some of my classmates came up to me and say: “Wow, how did you come up with that?“, “Wow, that was amazing thinking on the spot!“, or similar comments. I just told them exactly what I did:
“I visualized the function in a different way.“
HR
